[previous][map][next]

2.4 Trigonometrische Funktionen

2.4.1 Winkel modulo [-p; p]

Gegeben:
 
a Richtungswinkel
Gesucht:
 
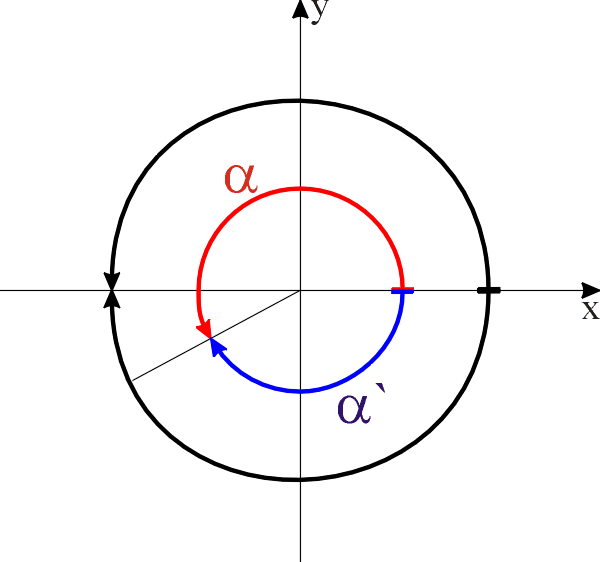
a` Richtungswinkel normiert auf den Bereich [-p; p]
Winkel werden im Bogenmaß angegeben. Zu Vergleichs- und Rechenzwecken müssen die Richtungswinkel auf den Bereich von [-p; p] normiert werden.
Ist der Winkel a größer als p, so könnte man so oft 2p von a abziehen, bis er kleiner als p wird. Dieses Vorgehen ist jedoch ineffizient, da insbesondere bei großen Winkeln viel Rechenzeit verschwendet wird, um den Winkel zu normieren. Es ist geschickter, im ersten Schritt a modulo 2p zu rechnen. Ist das Ergebnis größer als p, dann muss noch 2p abgezogen werden. Durch diese Maßnahme erhält man den Komplementärwinkel a` zu a.
Analog geht man bei Winkeln kleiner als -p vor. Als erstes rechnet man wieder modulo 2p. Ist das Ergebnis kleiner als -p, so addiert man 2p dazu.
Dadurch erhält man den normierten Winkel a`.
Rechnet man nur modulo p, so erhält man unter Umständen Winkel, die sich um p vom gewünschten Winkel unterscheiden, daher muss nach obiger Methode vorgegangen werden.

2.4.2 Winkel zwischen zwei Geraden

Gegeben:
 
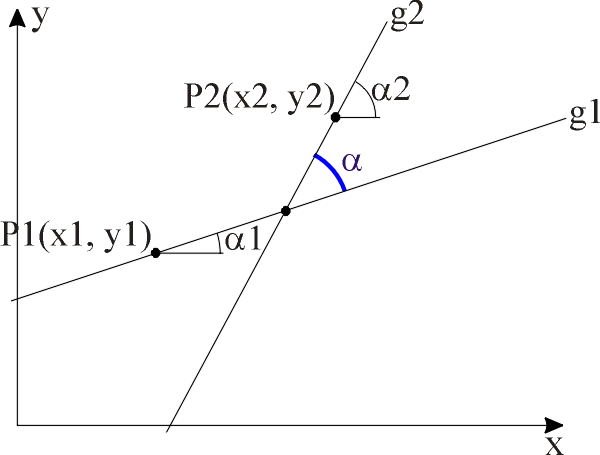
P1(x1, y1) Koordinaten eines Punktes auf der Gerade g1
a1 Richtungswinkel der Gerade g1
P2(x2, y2) Koordinaten eines Punktes auf der Gerade g2
a2 Richtungswinkel der Gerade g2
Gesucht:
 
a Winkel zwischen den Geraden
Zur Berechnung des von zwei Geraden eingeschlossenen Winkels verwendet man folgenden Algorithmus.
 
Ist a1 < a2 ?
 Ja
Nein 
Ist a1 - a2  < - p ?
 Ja
Nein 
 a = p - (a2 - a1) modulo p  a = a2 - a1
 a = (a2 - a1) modulo p

Diese Funktion liefert immer den kleinsten Winkel, der andere Winkel ergibt sich, indem man p - a rechnet.

2.4.3 Größe des Drehwinkels

Gegeben:
 
a1 Richtungswinkel bei Beginn der Drehung
a2 Richtungswinkel bei Ende der Drehung
d Drehrichtung
Gesucht:
 
a Überstrichener Winkel
Ein ähnliches Problem wie die Berechnung des von zwei Geraden eingeschlossenen Winkels ist die Berechnung des Drehwinkels. Zusätzlich spielt hier noch die Drehrichtung eine Rolle. Die Berechnung des Drehwinkels wird kompliziert, sobald man bei der Drehung die Richtungswinkel p bzw. -p überstreicht.
Es ergibt sich folgender Algorithmus.
 
Normiere Startrichtung sr
Normiere Endrichtung er
Haben sr und er gleiches Vorzeichen?
 Ja
Nein 
Drehwinkel dw = er - sr  Drehwinkel dw = (er - sr + 2p) modulo 2p
dw < 0 und Linksdrehung
 Ja
Nein 
dw += 2p
dw > 0 und Rechtsdrehung
 Ja
Nein 
dw -= 2p  
dw < 0 und Linksdrehung
 Ja
Nein 
dw += 2p
dw > 0 und Rechtsdrehung
 Ja
Nein 
dw -= 2p  
dw = dw modulo 2p

 

2.4.4 Winkel im Drehbereich

Gegeben:
 
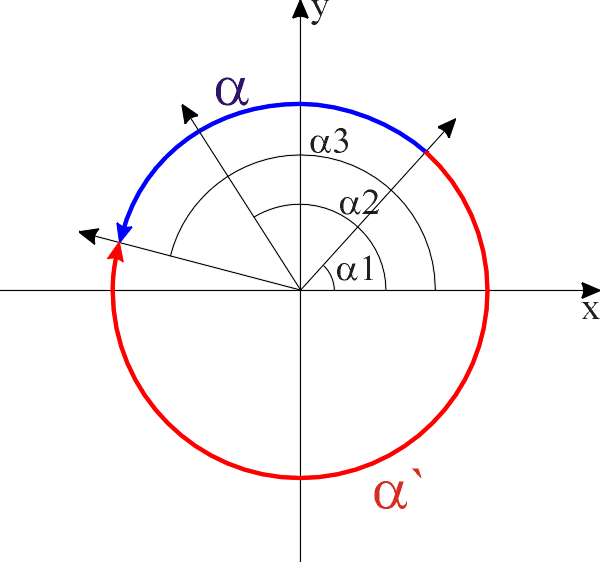
a1 Richtungswinkel bei Start der Drehung
a2 Richtungswinkel bei Ende der Drehung
a3 Richtungswinkel in Zwischenpunkt
d Drehrichtung
Gesucht:
 
Wird bei der Drehung der Richtungswinkel des Zwischenpunktes überstrichen?
Man sieht in Richtung a1 und dreht sich dann in Drehrichtung, bis man in Richtung a3 sieht. Überstreicht man dabei die Richtung mit dem Richtungswinkel a2, so liefert diese Funktion true ansonsten false. Ist die Drehrichtung a, so ist der Rückgabewert der Funktion true. Dies ist in obiger Abbildung blau dargestellt. Ist die Drehrichtung im Uhrzeigersinn, also a`, so wird der Richtungswinkel nicht überstrichen. Dies ist rot dargestellt. Zur Berechnung des Rückgabewertes geht man wie folgt vor.
 
Berechnung des Drehwinkels Start bis Zwischenrichtung l
Berechnung des Drehwinkels Start bis Ende der Drehung (a bzw. a`)
Ist der Absolutwert von l kleiner als der Absolutwert von a bzw. a`?
 Ja
Nein 
Zwischenpunkt wird überstrichen Zwischenpunkt wird nicht überstrichen

[previous][map][next]