Gesucht:
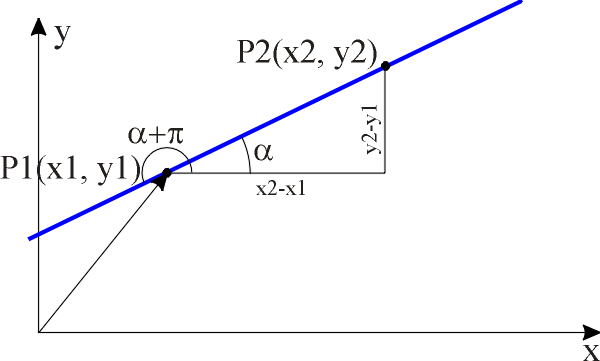
P1 (x1, y1) Koordinaten des 1. Punktes auf der Geraden P2 (x2, y2) Koordinaten des 2. Punktes auf der Geraden
Eine Gerade ist durch zwei nicht identische Punkte P1 und P2 eindeutig bestimmt. Da jedoch Geraden in meinem Programm in einer Punkt-Winkel-Form verwaltet werden, ist die Berechnung des Richtungswinkels der Gerade nötig.
P(x, y) Koordinaten eines Punktes der Geraden a Richtungswinkel der Geraden
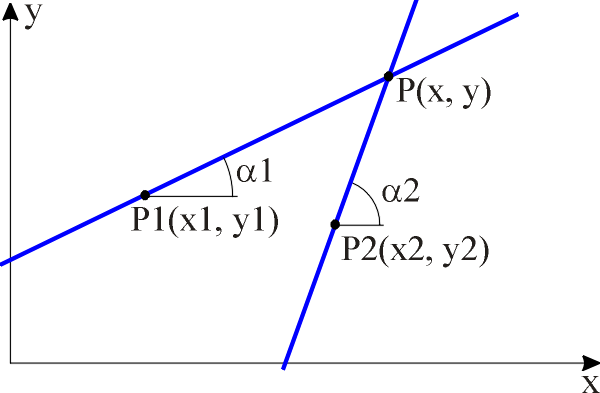
Gerade 1:Gesucht:
P1(x1, y1) Koordinaten eines Punktes auf der Gerade 1 a1 Richtungswinkel der Gerade 1 Gerade 2:
P2(x2, y2) Koordinaten eines Punktes auf der Gerade 2 a2 Richtungswinkel der Gerade 2
Zwei Geraden schneiden sich in einem Punkt, wenn sie nicht parallel sind. Sind die Geraden parallel, muss eine Ausnahmebehandlung durchgeführt werden. Den Schnittpunkt der Geraden erhält man folgendermaßen:
P(x, y) Koordinaten des Schnittpunktes
s1 = tan(a1)Auch hier ist eine Sonderbehandlung für a = 90° bzw. 270° nötig, da für diese Werte die Tangensfunktion nicht definiert ist.
s2 = tan(a2)
a1 = y1 - s1 * x1Die Koordinaten des Schnittpunktes ergeben sich wie folgt:
a2 = y2 - s2 * x2
x = (a2 - a1) / (s1 - s2)Sollte eine der Geraden parallel zur y-Achse sein, so kann der y-Achsenabschnitt nicht berechnet werden, es muss daher anders verfahren werden. Der x-Wert des Schnittpunktes entspricht dem x-Wert der zur y-Achse parallelen Gerade, der y-Wert ergibt sich durch Einsetzen des x-Wertes in die Geradengleichung der anderen Gerade.
y = (s1 * a2 - s2 * a1) / (s1 - s2)
Gesucht:
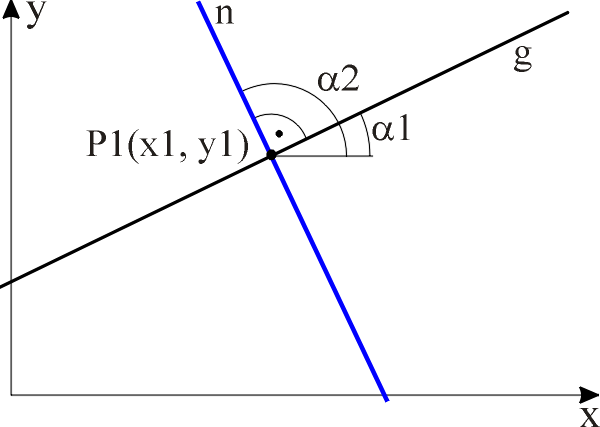
P1(x1, y1) Koordinaten eines Punktes auf der Gerade g a1 Richtungswinkel der Gerade g
Die Berechnung einer Normalen ist ohne großen Aufwand möglich. Für den Punkt P können die Koordinaten des Punktes P1 verwendet werden. Der Winkel a2 ergibt sich durch Addition von p/2 zum Richtungswinkel a1
P(x, y) Koordinaten eines Punktes auf der Normalen n a2 Richtungswinkel der Normalen n
P = P1Auch hier wurde zur Vereinfachung späterer Algorithmen der Richtungswinkel der Normalen durch a2 = a1 + p/2 festgelegt, also eine Drehung gegen den Uhrzeigersinn. Mathematisch richtig ist auch a2 = a1 - p/2.
a2 = a1 + p/2
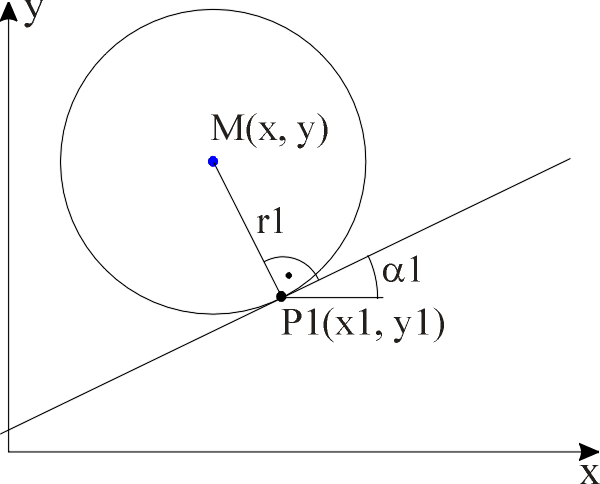
Gesucht:
P(x1, y1) Koordinaten eines Punktes auf dem Kreis a1 Tangentenwinkel im Punkt P r1 Radius im Punkt P
Gegeben ist ein Punkt auf dem Gleis. Es ist die Richtung des Gleises in diesem Punkt bekannt. Weiterhin kennt man die Krümmung, also den Radius an dieser Stelle des Gleises. Gesucht ist das Zentrum zu dem zugehörigen Radius.
M(x, y) Koordinaten des Kreismittelpunktes
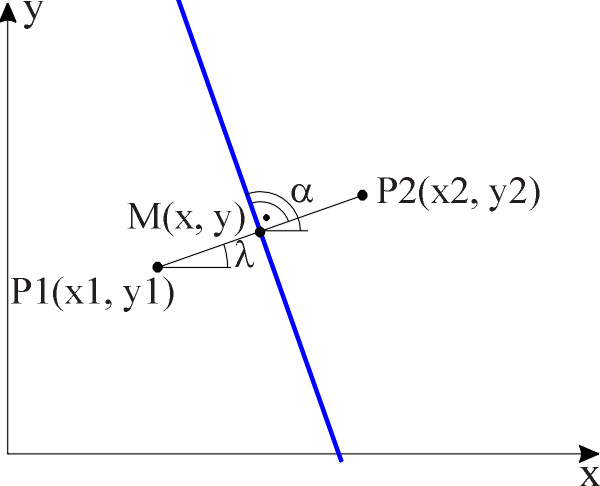
Gesucht:
P1(x1, y1) Koordinaten eines Punktes P1 P2(x2, y2) Koordinaten eines Punktes P2
Für diverse Programmteile ist die Berechnung der Mittelsenkrechte zwischen zwei Punkten nötig. Diese berechnet sich auf folgende Weise:
M(x, y) Koordinaten des Mittelpunktes zwischen P1 und P2 a Richtungswinkel der Mittelsenkrechten
Gesucht:
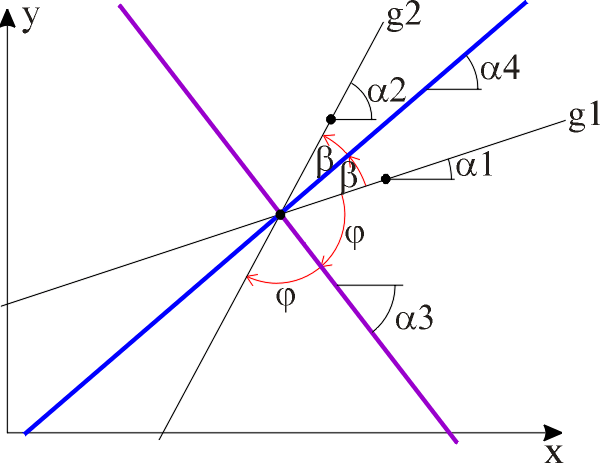
P1(x1, y1) Koordinaten eines Punktes auf der Gerade g1 a1 Richtungswinkel der Gerade g1 P2(x2, y2) Koordinaten eines Punktes auf der Gerade g2 a2 Richtungswinkel der Gerade g2
Die Koordinaten des Punktes M erhält man, indem man die Geraden g1 und g2 schneidet.
M(x, y) Koordinaten eines Punktes auf der Normalen n a Richtungswinkel der Normalen n